线性规划模型及概念

  • LP标准型：（mm rows × nn columns）

max⁡z=∑j=1ncjxjs. t.∑j=1naijxj=bi,i=1,2,…,mxj≥0,j=1,2,…,n\begin{array}{ll} \max & z = \sum\limits_{j=1}^n c_j x_j \\ \text{s. t.} & \sum \limits_{j=1}^n a_{ij} x_j = b_i, \quad i = 1, 2, \dots, m \\ & x_j \ge 0, \quad j = 1, 2, \dots, n \end{array}

几种特殊情况下的标准化方法：

  1. 目标函数为 minmin：minZ=max(−Z)min Z = max (-Z)
  2. bi<0b_i<0：等式两边同乘（-1）
  3. 约束条件为不等式：引入松弛变量
  4. 变量无约束：令 x=x′−x′′x=x'-x'' ，则有 x′,x′′>0x',x''>0
    注：若同时含两个及以上变量无约束，可利用形如 x1=x1′−x′′x_1=x_1'-x''、x2=x2′−x′′x_2=x_2'-x'' 来减少变量个数
  5. 变量 ≤0\leq0：令 x′=−xx'=-x ，则有 x′≥0x'\geq0

注：引入新变量时要将新变量回代到方程组中
例：x0≥1→x1=x0−1≥0x_0\geq1\to x_1=x_0-1\geq0，需回代 x0=x1+1x_0=x_1+1

若 KK 是 nn 维欧式空间的一个点集，∀x1,x2∈K\forall x_1,x_2 \in K，则 X=αX1+(1−α)X2  (0≤α≤1),X∈KX=\alpha X_1+(1-\alpha)X_2\;(0\leq\alpha\leq1),X \in K，称K为凸集。

凸集判断方法：任意两点连成一条直线，均在区域内可判断为凸集，否则不是。

灵敏度分析

  • 灵敏度：系统因周围环境变化显示出来的敏感程度
  • 两个问题：
    1. 参数中的一个或多个发生变化，现行最优方案会发生什么变化？
    2. 将这些参数的变化控制在什么范围内，原最优解仍最优？

基本性质

  1. 若线性规划问题存在可行域，则为凸集（图解法便于理解）
  2. 标准型LP问题一定有基解
  3. 若线性规划问题存在多个最优解，至少有两个相邻的基可行解（图解法，目标函数移动到最高点时与边界重合。

图解法

将标准型化为典式，其s.t.系数矩阵需含有与约束条件个数相同的同阶满秩单排列方阵。
例：

{100a11a12a13010a21a22a23001a31a32a33}\begin{Bmatrix} 1 & 0 & 0 & a_{11} & a_{12} & a_{13}\\ 0 & 1 & 0 & a_{21} & a_{22} & a_{23}\\ 0 & 0 & 1 & a_{31} & a_{32} & a_{33}\\ \end{Bmatrix}

注：原方程中s.t.约束条件在图中表现形式为取等时的函数图像。
一般绘制函数图像时仅有 2 ∼\sim 3 条坐标轴可供选择（直角、空间坐标系），故只在线性规划问题决策变量数为 2 或 3 时考虑使用图解法。这里仅对直角坐标系进行讨论。

  • 可行解：满足约束条件的解
  • 可行域：所有可行解构成的集合
  • 最优解：使目标函数最大的可行解
  • 基解：非基变量 XN=0X_N=0 ，为LP关于确定的基B的解

在图像中，约束条件函数图像上的点满足引入松弛变量为0的要求；而处于坐标轴上的点又满足至少一个决策变量为0的要求；因此，在直角坐标系中，图像上所有包含坐标轴与函数图像的交点，均为基解，因为其等价于非基变量为0。

然而，基解并不一定可行，因为它仅对非基变量提出非负的要求，而未对基变量做出要求，基变量仍需要“非负”的约束。

  • 两种判断基解是否可行的方法：

    1. 基变量非负即为基可行解
    2. 位于图中可行域内

  • 最优解
    最优解一定是基可行解，将目标函数 z=ax1+bx2+cz=ax_1+bx_2+c 中 zz 看作常数，转化为：x2=−abx1+z−cbx_2=-\frac{a}{b}x_1+\frac{z-c}{b}，要使 zz max，函数图像上移至可行域最高点；若存在最优解，则一定位于顶点处；此外，可能有无界解/无穷解导致最优解不存在。

线性规划模型求解及应用

MATLAB求解

1. 基于求解器求解

  • 规定标准形式：

min⁡xfTx\min x f^T x

s. t.{A⋅x≤b,Aeq⋅x=beq,lb≤x≤ub.\text{s. t.} \begin{cases} A \cdot x \le b, \\ A_{eq} \cdot x = b_{eq}, \\ lb \le x \le ub. \end{cases}

符号 说明
ff 价值向量
bb 资源向量
AA 不等式约束矩阵
AeqA_{eq} 等式约束矩阵

*f,x,b,beq,lb,ubf,x,b,b_{eq},lb,ub为列向量

  • 函数调用格式
1
2
3
[x,fval] = linprog(f,A,b);
[x,fval] = linprog(f,A,b,Aeq,beq);
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub);

其中 xx 将返回决策向量最优解，fvalfval 将返回最优值

2. 基于问题求解
先用向量和表达式构造优化问题，再用 solve 函数求解。

3. 对比

例：

max⁡z=2x1+3x2−5x3s. t.{x1+x2+x3=7,2x1−5x2+x3≥10,x1+3x2+x3≤12,x1,x2,x3≥0.\begin{array}{ll} \max & z = 2x_1 + 3x_2 - 5x_3 \\ \text{s. t.} & \begin{cases} x_1 + x_2 + x_3 = 7, \\ 2x_1 - 5x_2 + x_3 \ge 10, \\ x_1 + 3x_2 + x_3 \le 12, \\ x_1, x_2, x_3 \ge 0. \end{cases} \end{array}

解：

  1. 基于求解器求解
    首先，转化为MATLAB标准型：

nw=−2x1−3x2+5x3n w = -2x_1 - 3x_2 + 5x_3

s. t.{[−25−1131][x1x2x3]≤[−1012],[1,1,1][x1x2x3]T=7,[000]T≤[x1x2x3]T.\text{s. t.} \begin{cases} \begin{bmatrix} -2 & 5 & -1 \\ 1 & 3 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \le \begin{bmatrix} -10 \\ 12 \end{bmatrix}, \\ \begin{bmatrix} 1, 1, 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}^\mathrm{T} = 7, \\ \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}^\mathrm{T} \leq \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}^\mathrm{T}. \end{cases} 

1
2
3
4
5
6
clc, clear, f = [-2; -3; 5];
a = [-2, 5, -1; 1, 3, 1]; b = [-10; 12];
aeq = [1, 1, 1]; beq = 7;
lb = zeros(3, 1)
[x, y] = linprog(f, a, b, aeq, beq, lb);
x, y = -y
  1. 基于问题求解
1
2
3
4
5
6
7
8
clc, clear
prob = optimproblem('ObjectiveSense', 'max');
x = optimvar('x', 3, 'LowerBound', 0);
prob.Objective = 2 * x(1) + 3 * x(2) - 5 * x(3);
prob.Constraints.con1 = x(1) + x(2) + x(3) == 7;
prob.Constraints.con2 = 2 * x(1) - 5 * x(2) + x(3) >= 10;
prob.Constraints.con3 = x(1) + 3 * x(2) + x(3) <= 12;
[sol, fval, flag, out] = solve(prob), sol.x

数学规划——可转化为线性规划的问题

例1：

min⁡∑i=1nci∣xi∣s. t.Ax≤b.\begin{array}{ll} \min & \sum \limits_{i=1}^n c_i|x_i| \\ \text{s. t.} & Ax \le b. \end{array}

取 ui=xi+∣xi∣2,vi=∣xi∣−xi2u_i = \frac{x_i + |x_i|}{2}, \quad v_i = \frac{|x_i| - x_i}{2} ，问题可转化为：

min⁡∑i=1nci(ui+vi)s. t.{A(u−v)≤bu,v≥0.\begin{array}{ll} \min & \sum \limits_{i=1}^n c_i(u_i + v_i) \\ \text{s. t.} & \begin{cases} A(u - v) \le b \\ u, v \ge 0. \end{cases} \end{array}

可进一步改写为：

min⁡∑i=1nci(ui+vi)s.t.{[A,−A][uv]≤b,u,v≥0.\begin{array}{ll} \min & \sum \limits_{i=1}^n c_i(u_i + v_i) \\ \text{s.t.} & \begin{cases} \begin{bmatrix} A , -A \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \le b, \\ u, v \ge 0. \end{cases} \end{array}

注：对于带绝对值的线性规划问题，为提高求解效率，尽量先手工进行线性化，再使用软件求解。

例2：

min⁡xi{max⁡yi∣εi∣},其中 εi=xi−yi\min_{x_i} \left\{ \max_{y_i} | \varepsilon_i | \right\}, \quad \text{其中 } \varepsilon_i = x_i - y_i

取 v=max⁡yi∣εi∣v=\underset{y_i}{\max} | \varepsilon_i | ，转化为：

min⁡  vs.t.{x1−y1≤v,x2−y2≤v,…,xn−yn≤vy1−x1≤v,y2−x2≤v,…,yn−xn≤v\begin{align*} \min &\; v \\ \text{s.t.} & \begin{cases} x_1 - y_1 \le v, x_2 - y_2 \le v, \dots, x_n - y_n \le v \\ y_1 - x_1 \le v, y_2 - x_2 \le v, \dots, y_n - x_n \le v \end{cases} \end{align*}

将给定的问题转化为标准形式需要引入松弛变量。 由于约束条件是 ≤\leq 类型，我们为每个不等式引入一个非负的松弛变量。 假设有 nn 个 xix_i 和 yiy_i 变量对。 引入 2n2n 个松弛变量，记为 sis_i 和 tit_i (i=1,…,n)，所有松弛变量均非负，问题可以改写为：

最小化： vv
服从约束条件：

xi−yi+si=v  (i=1,...,n)x_i - y_i + s_i = v \; (i = 1, ..., n)

yi−xi+ti=v  (i=1,...,n)y_i - x_i + t_i = v \; (i = 1, ..., n)

si≥0,ti≥0  (i=1,...,n)s_i ≥ 0, t_i ≥ 0 \; (i = 1, ..., n)

令：

x=[x1,x2,...,xn,y1,y2,...,yn,v,s1,...,sn,t1,...,tn]T(一个  3n+1  维向量)x = [x_1, x_2, ..., x_n, y_1, y_2, ..., y_n, v, s_1, ..., s_n, t_1, ..., t_n]^T \quad (一个 \;3n+1\; 维向量)

c=[0,0,...,0,1,0,...,0]T(一个  3n+1  维向量，只有  v  的系数为1)c = [0, 0, ..., 0, 1, 0, ..., 0]^T \quad (一个 \;3n+1\; 维向量，只有\;v\;的系数为1)

那么目标函数为 cTxc^Tx，我们可以将其表示为矩阵形式，所有变量都隐含着非负约束 x≥0x \geq 0。

1998年全国大学生数学建模竞赛A题

  • 问题背景: 某公司拥有 MM 资金，需要在 nn 种资产中进行投资，以期获得最大收益并最小化风险。
  • 资产特征: 每种资产 SiS_i (i=1,2,…,ni=1,2,\dots,n) 具有以下特征：
    • 平均收益率：rir_i
    • 风险损失率：qiq_i
    • 交易费率：pip_i (当购买额不超过 uiu_i 时，按 uiu_i 计算交易费；超过则按实际购买额计算)
  • 风险度量: 投资组合的总体风险定义为所投资资产中最大风险损失率的最大值。
  • 无风险投资: 存在一种无风险投资，即银行存款，利率为 r0=0.05r_0 = 0.05，无交易费用。
  • 目标: 在给定资金 MM 和资产特征的情况下，确定最佳的投资组合，即每种资产的投资额 xix_i，以最大化收益并最小化风险。
  • 约束条件:
    • ∑i=1nxi≤M\sum_{i=1}^n x_i \le M (总投资额不超过可用资金)
    • xi≥0x_i \ge 0 (投资额非负)
  • 已知条件: 问题给出了 n=4n=4 时各资产的相关数据。
SiS_i rir_i /% qiq_i /% pip_i /% uiu_i /元
S1S_1 28 2.5 1 103
S2S_2 21 1.5 2 198
S3S_3 23 5.5 4.5 52
S4S_4 25 2.6 6.5 40

问题分析

这是一个组合投资问题：已知市场上可供投资的 n+1 种资产（n种资金和银行）的平均收益率、风险损失率及交易费率，要求设计一种投资组合方案，将可供投资的资金分成数量不等的 n+1 份，分别购买 n+1 种资产。不同类型资产的平均收益率和风险损失率也各不相同，因此在进行投资时要同时兼顾两个目标：投资净收益和风险。

符号说明

符号 说明
SiS_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 可供投资的n+1项资产，其中 S0S_0 代表银行
xix_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 投资到资产 SiS_i 的资金数量
rir_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 资产 SiS_i 的平均收益率
qiq_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 资产 SiS_i 的风险损失率
pip_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 资产 SiS_i 的交易费率
uiu_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 资产 SiS_i 的投资阈值
mim_i，i=0,1,⋅⋅⋅,ni=0,1,···,n 投资到资产 SiS_i 的交易费
qzq_z 总体风险

模型假设

  1. 可供投资的金额 M 相当大
  2. 投资越分散，总的风险就越小，总的风险用所投资的 SiS_i 中最大的风险表示
  3. 可供选择的 n+1 种资产之间相互独立
  4. 每种资产可购买的数量为任意值
  5. 当前投资周期内，rir_i、qiq_i、uiu_i（i=0,1,⋅⋅⋅,ni=0,1,···,n）固定不变
  6. 不考虑资产交易过程中产生的的其他额外费用

模型建立

qz=max⁡{qi∣xi>0}q_z = \max\{q_i | x_i > 0\}

si={piuixi≤uipixixi>uis_i= \begin{cases} p_iu_i & x_i \leq u_i \\ p_ix_i & x_i>u_i \\ \end{cases}

题目所给定值 uiu_i 相对于总投资 MM 很少，piuip_i u_i 也很少，这样购买 SiS_i 的总收益可以简化为：

(ri−pi)xi(r_i-p_i)x_i

要使净收益尽可能大，总体风险尽可能小，这是一个多目标规划模型。

目标函数

{max⁡  ∑i=0n(ri−pi)ximin⁡  {  max⁡1≤i≤n{qixi}  }\begin{cases} \max \; \sum \limits_{i=0}^{n} (r_i - p_i)x_i \\ \min \;\{\;\underset{1 \le i \le n}{\max } \{q_i x_i\}\;\} \end{cases}

约束条件

{∑i=0n(1+pi)xi=Mxi≥0,i=0,1,…,n\begin{cases} \sum \limits_{i=0}^{n} (1 + p_i)x_i = M \\ x_i \ge 0, \quad i = 0, 1, \dots, n \end{cases}

模型简化

  1. 实际投资中投资者承受的风险不一样，若给定一个风险值 aa，使最大的一个风险 qixiM≤a\frac{q_ix_i}{M}\leq a，即可找到相应投资方案，就将多目标规划转化为一个目标的线性规划。

max⁡∑i=0n(ri−pi)xi\max \sum \limits_{i=0}^{n} (r_i - p_i)x_i

s. t.{qixiM≤a,i=1,2,…,n∑i=0n(1+pi)xi=Mxi≥0,i=0,1,…,n\text{s. t.} \begin{cases} \frac{q_i x_i}{M} \le a, & i = 1, 2, \dots, n \\ \sum \limits_{i=0}^{n} (1 + p_i)x_i = M \\ x_i \ge 0, & i = 0, 1, \dots, n \end{cases}

  1. 投资者希望总盈利至少达到水平 kk 以上，在风险最小的情况下寻求相应投资组合。

min⁡{max⁡1≤i≤n{qixi}},\min \left\{ \underset{1 \le i \le n}{\max} \{q_i x_i\} \right\},

s. t.{∑i=0n(ri−pi)xi≥kM,∑i=0n(1+pi)xi=M,xi≥0,i=0,1,…,n\text{s. t.} \begin{cases} \sum\limits_{i=0}^{n} (r_i - p_i)x_i \ge kM, \\ \sum\limits_{i=0}^{n} (1 + p_i)x_i = M, \\ x_i \ge 0, & i = 0, 1, \dots, n \end{cases}

  1. 投资者在权衡资产收益和预期收益两方面时，希望选择一个令自己满意的投资组合。

min⁡w{max⁡1≤i≤n{qixi}}−(1−w)∑i=0n(ri−pi)xi,\min w \left\{ \underset{1 \le i \le n}{\max} \{q_i x_i\} \right\} - (1 - w) \sum\limits_{i=0}^{n} (r_i - p_i)x_i,

s. t.{∑i=0n(1+pi)xi=M,xi≥0,i=0,1,…,n\text{s. t.} \begin{cases} \sum\limits_{i=0}^{n} (1 + p_i)x_i = M, \\ x_i \ge 0, & i = 0, 1, \dots, n \end{cases}

模型求解与分析

为简化计算，求解时不妨令 M=10000M=10000 元

模型一

max⁡f=[0.05,0.27,0.19,0.185,0.185]⋅[x0x1x2x3x4]T,s. t.{x0+1.01x1+1.02x2+1.045x3+1.065x4=M,0.025x1≤aM,0.015x2≤aM,0.055x3≤aM,0.026x4≤aM,xi≥0 (i=0,1,…,4).\begin{array}{ll} \max &f = [0.05, 0.27, 0.19, 0.185, 0.185] \cdot \begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}^\mathrm{T}, \\ \text{s. t.} &\begin{cases} x_0 + 1.01x_1 + 1.02x_2 + 1.045x_3 + 1.065x_4 = M, \\ 0.025x_1 \le aM, \\ 0.015x_2 \le aM, \\ 0.055x_3 \le aM, \\ 0.026x_4 \le aM, \\ x_i \ge 0 \ (i = 0, 1, \dots, 4). \end{cases} \end{array}

aa 是任意给定的风险度，没有具体准则，不同投资者有不同的风险度偏好。我们从 a=0a = 0 开始，以步长 Δa=0.001\Delta a = 0.001 进行循环搜索，编制程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
clc, clear, close all
prob = optimproblem('ObjectiveSense','max');
x = optimvar('x',5,1,'LowerBound',0);
c = [0.05,0.27,0.19,0.185,0.185]; % 净收益率
Aeq = [1,1.01,1.02,1.045,1.065]; % 等约束矩阵
prob.Objective = c*x; M = 10000;
prob.Constraints.con1 = Aeq*x == M;
q = [0.025,0.015,0.055,0.026]'; % 风险损失率
a = 0; aa = []; QQ = []; XX = []; hold on
while a<0.05
prob.Constraints.con2 = q.*x(2:end)<=a*M;
[sol,Q,flag,out] = solve(prob);
aa = [aa; a]; QQ = [QQ, Q];
XX = [XX; sol.x']; a=a+0.001;
end
plot(aa,QQ,'*k')
xlabel('$a$','Interpreter','Latex')
ylabel('$Q$','Interpreter','Latex', 'Rotation',0)

风险 a 与收益 Q 之间的关系如图：

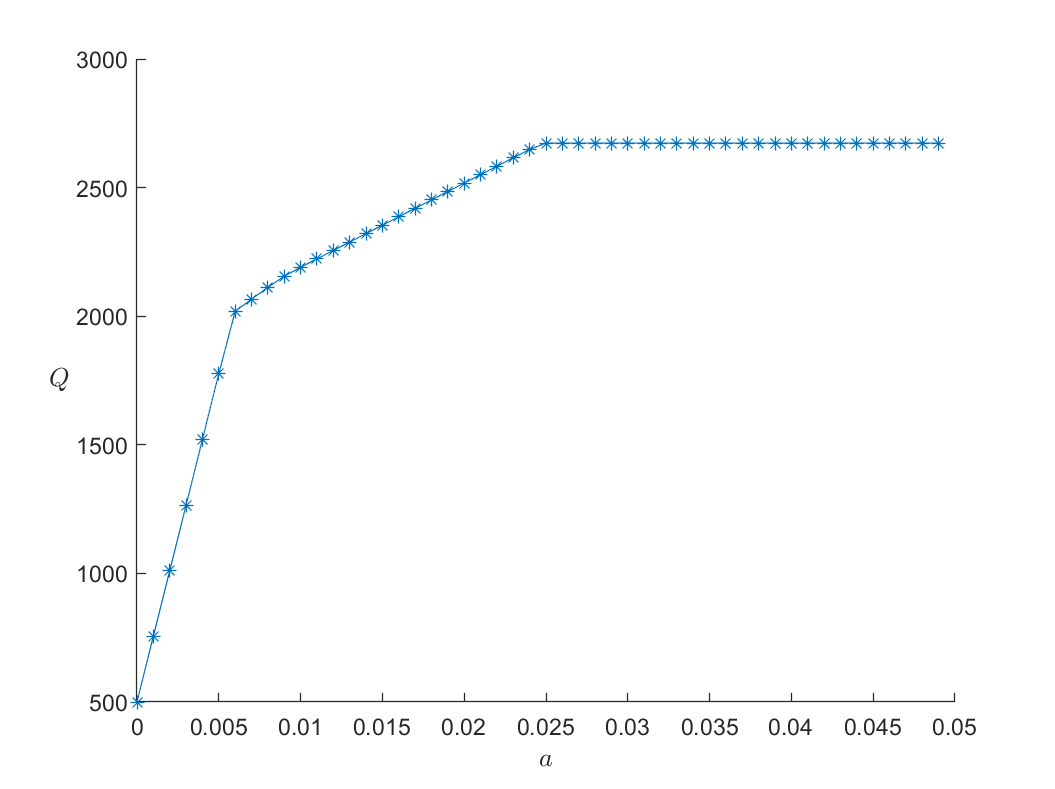
(1) 风险大，收益也大
(2) 投资越分散，投资者承担的风险越小，这与题意一致。冒险的投资者会出现集中投资的i情况，保守的投资者则尽量分散投资。
(3) 在 a=0.006 附近有一个转折点，这点的左边风险增加得很少时，收益增长得很快；右边风险增加得很大时，收益增长得很慢。因此对于风险和收益没有特殊偏好的投资者来说，应选择曲线的转折点作为最优投资组合，大约是 a=0.6%，Q=2000，对应的投资方案为：

a=0.006,Q=2019,x0=0,x1=2400,x2=4000,x3=1091,x4=2212a=0.006,Q=2019,x_0=0,x_1=2400,x_2=4000,x_3=1091,x_4=2212

模型二

取 x5=max⁡1≤i≤5{qixi}x_5=\underset{1 \le i \le 5}{\max} \{q_i x_i\}

min⁡x5  ,s. t.{x0+1.01x1+1.02x2+1.045x3+1.065x4=M,0.05x0+0.255x1+0.195x2+0.175x3+0.224x4≥kM,2.5x1≤x5,1.5x2≤x5,5.5x3≤x5,2.6x4≤x5,xi≥0,i=0,1,…,5\begin{array}{ll} \min & x_5 \;, \\ \text{s. t.} & \begin{cases} x_0 + 1.01x_1 + 1.02x_2 + 1.045x_3 + 1.065x_4 = M, \\ 0.05x_0 + 0.255x_1 + 0.195x_2 + 0.175x_3 + 0.224x_4 \geq kM, \\ 2.5 x_1 \le x_5, \\ 1.5 x_2 \le x_5, \\ 5.5 x_3 \le x_5, \\ 2.6 x_4 \le x_5, \\ x_i \ge 0, i = 0, 1, \dots, 5 \\ \end{cases} \end{array}

k是任意给定的盈利水平率，我们从 k=1k = 1 开始，以步长 Δa=0.1\Delta a = 0.1 进行循环搜索，编制程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
clc, clear, close all
M = 10000;
% 初始化存储结果的数组
KK = []; % 盈利水平
VV = []; % 风险
XX = []; % 投资方案
% 从k = 0开始，步长为0.01，搜索不同的盈利水平
for k = 0:0.01:0.25
prob = optimproblem('ObjectiveSense', 'min');
x = optimvar('x', 6, 1, 'LowerBound', 0);
% 约束条件
prob.Constraints.con1 = x(0+1) + 1.01*x(1+1) + 1.02*x(2+1) + 1.045*x(3+1) + 1.065*x(4+1) == M;
prob.Constraints.con2 = 0.05*x(0+1) + 0.255*x(1+1) + 0.195*x(2+1) + 0.175*x(3+1) + 0.224*x(4+1) >= k*M;
% 风险约束
prob.Constraints.con3 = 2.5*x(1+1) <= x(5+1);
prob.Constraints.con4 = 1.5*x(2+1) <= x(5+1);
prob.Constraints.con5 = 5.5*x(3+1) <= x(5+1);
prob.Constraints.con6 = 2.6*x(4+1) <= x(5+1);
% 目标函数：最小化x5（最大风险）
prob.Objective = x(5+1);
% 求解
[sol, fval, flag, out] = solve(prob);
% 存储结果
KK = [KK, k];
VV = [VV, fval];
XX = [XX, sol.x'];
end
% 绘制盈利水平与风险的关系
plot(KK, VV, '*-');
xlabel('盈利水平 k');
ylabel('风险');
title('盈利水平与风险的关系');
grid on
% 输出结果
disp('盈利水平:');
disp(KK);
disp('对应风险:');
disp(VV);

风险与盈利水平 k 之间的关系如图：

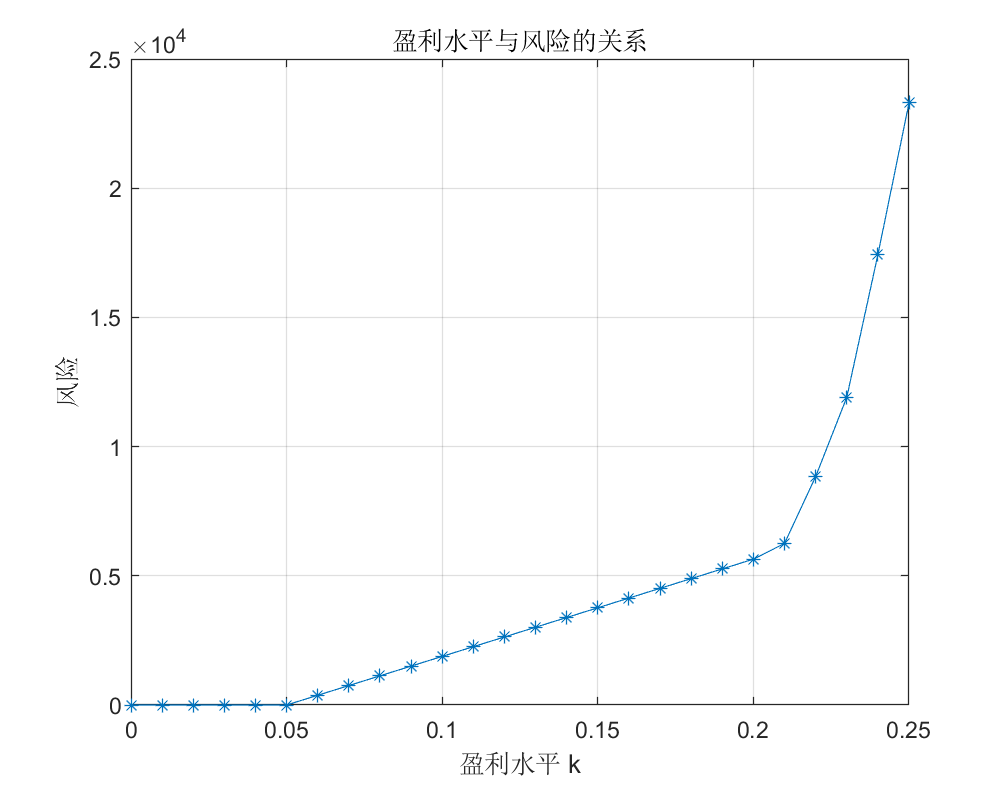
模型三

具体求解时需要将目标函数线性化，引进变量 xn+1=max⁡1≤i≤n{qixi}x_{n+1}=\underset{1 \le i \le n}{\max} \{q_i x_i\} ，转化为：

min⁡wxn+1−(1−w)∑i=0n(ri−pi)xis. t.{qixi≤xn+1,i=1,2,…,n,∑i=0n(1+pi)xi=10000,xi≥0,i=0,1,2,…,n.\begin{align*} \min \quad & wx_{n+1} - (1 - w) \sum_{i=0}^{n} (r_i - p_i)x_i \\ \text{s. t.} \quad & \begin{cases} q_i x_i \le x_{n+1}, & i = 1, 2, \dots, n, \\ \sum\limits_{i=0}^{n} (1 + p_i)x_i = 10000, \\ x_i \ge 0, & i = 0, 1, 2, \dots, n. \end{cases} \end{align*}

可求得当 ww 取不同值时风险和收益的计算结果如下表：

w 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
风险 247.52 247.52 247.52 247.52 247.52 247.52 247.52 247.52 92.25 59.4 0
收益 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2673.27 2164.82 2016.24 500

当投资偏好系数 w≤0.7w\leq 0.7时，所对应的收益和风险均达到最大值，此时，收益为 2673.27 元，风险为 247.52 元，全部资金均用来购买资产 S1S_1 ；当 ww 由 0.7 增加到1.0 时，收益和风险均呈下降趋势；特别地，当 w=1.0w=1.0 时，收益和风险均达到最小值，收益为 500 元，风险为 0 元，此时应将所有资金全部存入银行。

为更好地描述收益和风险的对应关系，可将 w 的取值进一步细化，重新计算的部分数据如表所示：

w 0.766 0.767 0.810 0.811 0.824 0.825 0.962 0.963 1.0
风险 247.52 92.25 95.25 78.49 78.49 59.4 59.4 0 0
收益 2673.27 2164.82 2164.82 2105.99 2105.99 2016.24 2016.24 500 500

绘制收益和风险的函数关系图像如图所示：

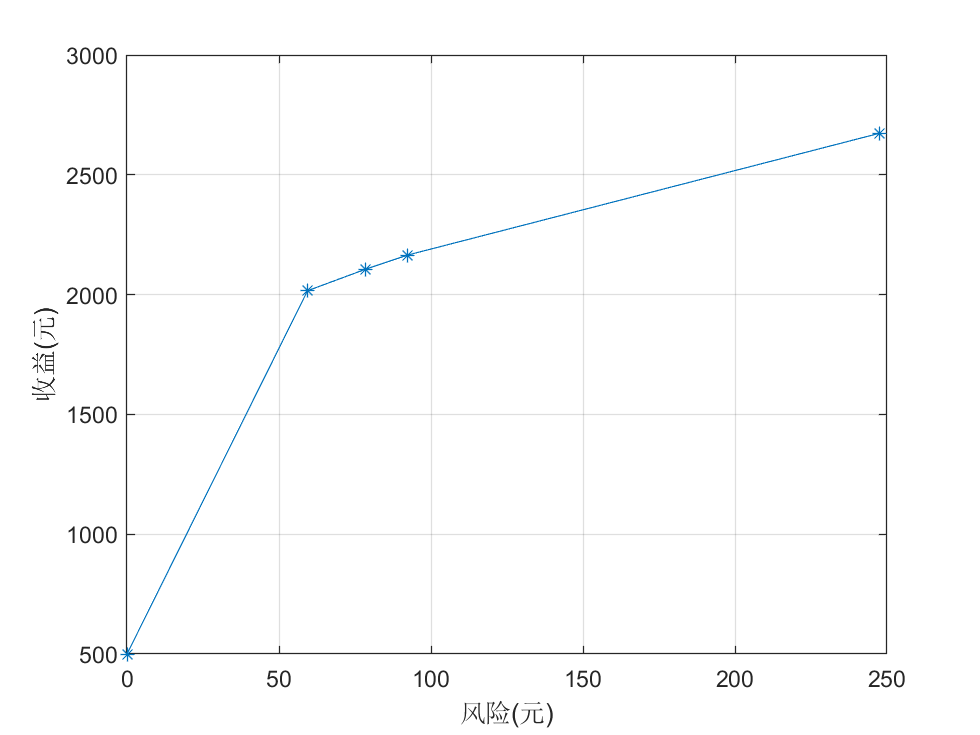
投资的收益越大，风险也越大。投资者可以根据自己对风险喜好不同的，选择合适的投资方案。曲线的拐点坐标约为 (59.4, 2016.24) ，此时对应的投资方案是购买资产S1S_1、S2S_2、S3S_3、S4S_4的资金分别为2375.84 元、3959.73 元、1079.93 元和2284.46 元，存入银行的资金为 0 元，这对于风险和收益没有明显偏好的投资者是一个比较合适的选择。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
clc, clear, close all, format long g
M = 10000; prob = optimproblem;
x = optimvar('x', 6, 1, 'LowerBound', 0);
r = [0.05, 0.28, 0.21, 0.23, 0.25]; % 收益率
p = [0, 0.01, 0.02, 0.045, 0.065]; % 交易费率
q = [0, 0.025, 0.015, 0.055, 0.026]'; % 风险损失率
w = [0.766, 0.767, 0.810, 0.811, 0.824, 0.825, 0.962, 0.963, 1.0]; % 风险初始化
V = []; % 收益初值化
Q = []; % 最优解的初始化
X = [];
prob.Constraints.con1 = (1 + p) * x(1:end - 1) == M;
prob.Constraints.con2 = q(2:end) .* x(2:end - 1) <= x(end);
for i = 1:length(w)
	prob.Objective = w(i) * x(end) - (1 - w(i)) * (r - p) * x(1:end - 1);
	[sol, fval, flag, out] = solve(prob);
	xx = sol.x;
	V = [V, max(q .* xx(1:end - 1))];
	Q = [Q, (r - p) * xx(1:end - 1)];
	X = [X, xx'];
	plot(V, Q, '*');
	grid on
	xlabel('风险(元)');
	ylabel('收益(元)')
end
V, Q, format